Finding the angle between two vectors

from numpy import linalg
import numpy as np


n=int(input('Vector in R(n): '))

list_of_first_v=[]
list_of_second_v=[]
for i in range(n):
    list_of_first_v.append(int(input('Number for 1st vector: ')))
for m in range(n):
    list_of_second_v.append(int(input('Number for 2nd vector: ')))

#Create the vectors
vector1=np.array([list_of_first_v])
vector2=np.array([list_of_second_v])

#Norm of the vectors
v1_norm=linalg.vector_norm(vector1)
v2_norm=linalg.vector_norm(vector2)

#Applying the formula
rhs=(np.vecdot(vector1,vector2)/(v1_norm*v2_norm))
cos_theta=rhs
#To find theta
theta=np.arccos(rhs)
if n==2:
    v1n=vector1[0]
    v2n=vector2[0]
    origin = np.array([[0, 0, 0],[0, 0, 0]])
    fig, ax = plt.subplots()
    ax.quiver(0, 0, v1n[0], v1n[1], angles='xy', scale_units='xy', scale=1, color='r', label='Vector 1')
    ax.quiver(0, 0, v2n[0], v2n[1], angles='xy', scale_units='xy', scale=1, color='b', label='Vector 2')
    ax.set_xlim([-10, 10])
    ax.set_ylim([-10, 10])
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    plt.grid()
    plt.axhline(y=0, color='k')
    plt.axvline(x=0, color='k')
    plt.show()
elif n==3:
    v1n=vector1[0]
    v2n=vector2[0]
    c1=[]
    c2=[]
    for i in range(0,3):
        c1.append(v1n[i])
        c2.append(v2n[i])
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')

    ax.quiver(0,0,0,v1n[0],v1n[1],v1n[2],color='b', label='Vector 1')
    ax.quiver(0,0,0,v2n[0],v2n[1],v2n[2],color='r', label='Vector 2')

    ax.set_xlim([-10, 10])
    ax.set_ylim([-10, 10])
    ax.set_zlim([-10, 10])
    ax.set_xlabel('X-axis')
    ax.set_ylabel('Y-axis')
    ax.set_zlabel('Z-axis')
    ax.set_title('Two 3D Vectors Plot')
    plt.show()

Assume that \( n:=3 \) that is our vectors will be in \( \mathbb{R}^3 \). Let \(v:=\begin{bmatrix}1 \\ 4 \\ 7 \end{bmatrix}\) and \(u:=\begin{bmatrix}2 \\ 3 \\ 8 \end{bmatrix}\).First of all let us calculate the inner product of two vectors v and u. \(u.v=(1,4,7).(2,3,8)=1*2+4*3+7*8=70\). Then length of the vector v is \(\left\| v \right\|=\sqrt{v.v}=\sqrt{(1,4,7).(1,4,7)}=\sqrt{66}\) and length of the vector u is \(\left\| u \right\|=\sqrt{u.u}=\sqrt{(2,3,8).(2,3,8)}=\sqrt{77}\)

Angle between the vectors is calculated by the formula which is appeared the above.

\(cos\theta=\frac{u.v}{\left\| u \right\|\left\| v \right\|}=\frac{70}{\sqrt{66}\sqrt{77}}=\frac{70}{66*77}=0.0137741046831956\). Then, angle is \(\theta=arccos(0.0137741046831956)=1.5570217865236389\).

By visualizing the vector, we obtain

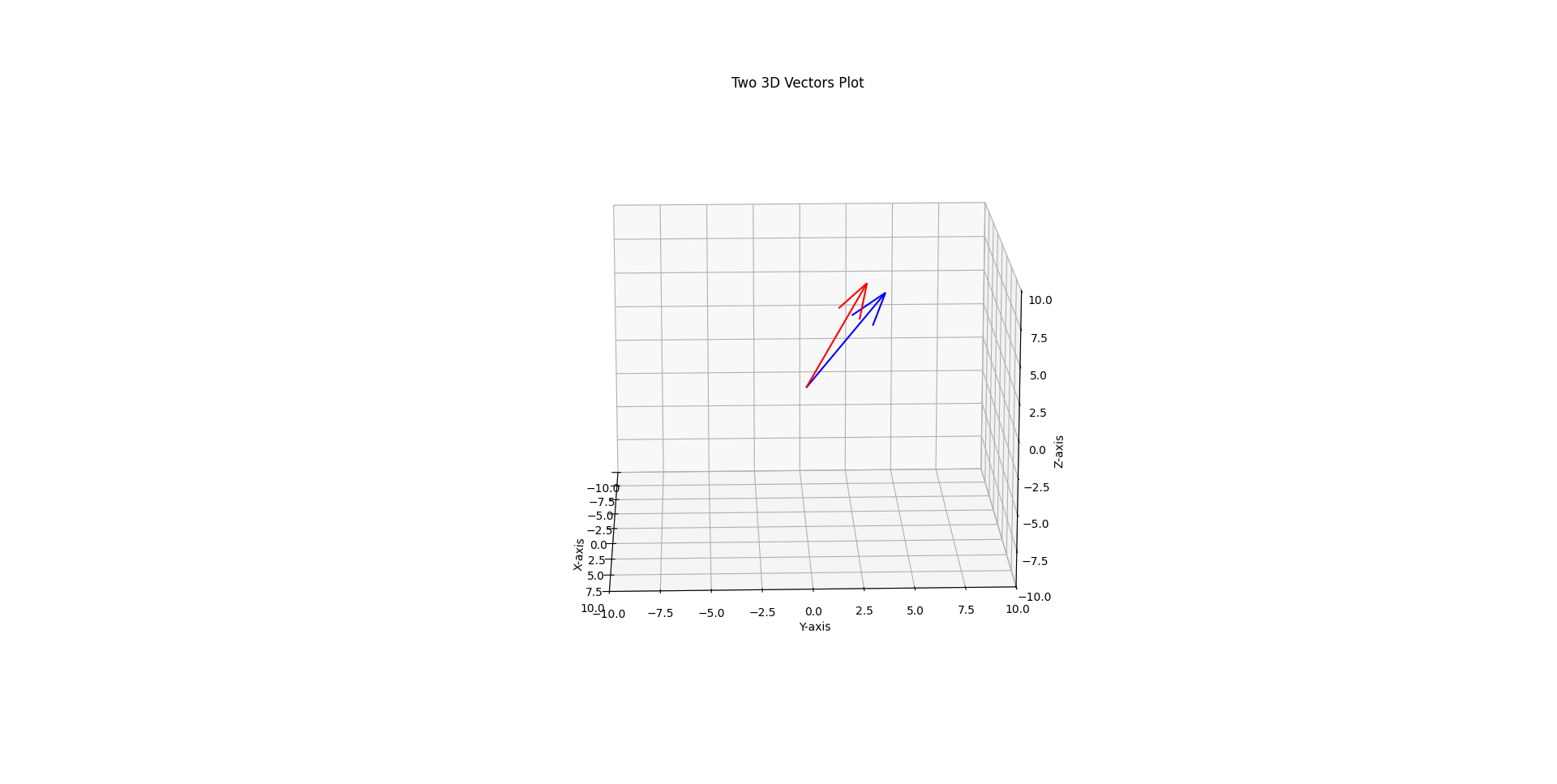
In this writing, I tried to find the angle between two given vectors and to visualize them if they are in \( \mathbb{R}^2 \) or \( \mathbb{R}^3 \). (You can also find the source code which is given with MATLAB by clicking here)

Finding the angle between two vectors with Python