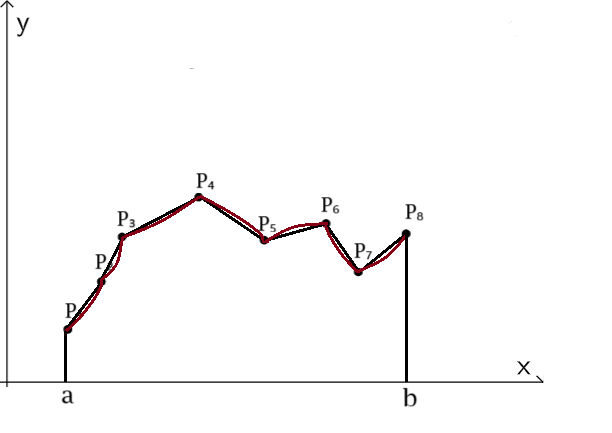

$$L \approx \sum\limits_{i = 2}^n {|{P_{i - 1}} - {P_i}|} $$
By taking n larger and larger we can get the result:
$$L = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 2}^n {|{P_{i - 1}} - {P_i}|} $$
Let us get a better approach the length of each of these line segments.
As we know from geometry, we can consider length of each of these line segments as:
$$\eqalign{ & \Delta {y_i} = {y_i} - {y_{i - 1}} \cr & \Delta {x_i} = {x_i} - {x_{i - 1}} \cr} $$
We can calculate the length of the line segments with this way:
$$|{P_i} - {P_{i - 1}}| = \sqrt {{{({x_i} - {x_{_{i - 1}}})}^2} + {{({y_i} - {y_{_{i - 1}}})}^2}} $$
$$ = \sqrt {\Delta {y_i}^2 + \Delta {x_i}^2} $$
$$\Delta {y_i} = f({x_i}) - f({x_{i - 1}}) = f\prime ({x_k})({x_i} - {x_{i - 1}})$$
$$\Delta {y_i} = f\prime ({x_k})\Delta x$$
To sum up, length can be written as:
$$|{P_{i - 1}} - {P_i}| = \sqrt {{{({x_i} - {x_{i - 1}})}^2} + {{({y_i} - {y_{i - 1}})}^2}} $$
$$ = \sqrt {\Delta {x^2} + {{[f\prime ({x_k})]}^2}\Delta {x^2}} $$
$$= \sqrt {1 + {{[f\prime ({x_k})]}^2}} \Delta x$$
Now we can calculate the exact length
$$L = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 2}^n {|{P_i} - {P_{i - 1}}|} $$
$$ = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 2}^n {\sqrt {1 + {{[f\prime ({x_k})]}^2}} } \Delta x$$
From the definition of the definite integral:
$$L = \int\limits_a^b {\sqrt {1 + {{[f\prime (x)]}^2}} dx} $$
i.e.
$$L = \int\limits_a^b {\sqrt {1 + {{({{dy} \over {dx}})}^2}} } dx$$
In a similar way, we can evaluate a formula for \({\mathop{\rm x}\nolimits} = g(y)\) on \([c,d]\).Formula is:
$$L = \int\limits_c^d {\sqrt {1 + {{[h\prime (y)]}^2}} } dy$$
It sometimes can be diffucult to calculate arc length without computer help. In this part, we will look at the sample python code to compute arc length